
Matrix theory
disclaimer
Matrices are linear functions for vectors. Consider U, V being vectors of any dimension.
Then U := M*V is transforming one vector (V) into another (U). Here, we further assume the
vectors being 3D vectors. A vector is not just a few numbers, it furthermore has a base
defining the system :
base
Here, as usual the base is a right hand euclidian system :
E1 = X = (1,0,0) E2 = Y = (0,1,0) E3 = Z = (0,0,1)
The base vectors of a coordinate system are orthogonal to each other in respect of
the applied scalar product (which is defined as '<a,b> = sum(ai*bi) over i' for this system),
e.g the scalarproduct of the base vectors is zero for all combinations.
There are other noneuclidian systems, such as the spherical one : (radius, longitude, latitude).
Note that also here, the 3 basevectors are locally right angled. The length of a base vector
is normalized to 1.
vectors
A vector defines a point in space with respect to the base.
P := x*E1 + y*E2 + z*E3
the (x,y,z) are called components of the vector and denote the partial content of each base vector.
The components are calculated formally as :
x:=<P,E1>, y:=<P,E2>, z:=<P,E3>
where <a,b> is again the scalar product, which in this case also is
|a|*|b|*cos(angle between), the product of the lengths times the cosine of the angle between.
matrices
Be V the old vector, M the matrix, and U the new vector :
U = M * V
or
|u1| |m11 m12 m13| |v1|
|u2| = |m21 m22 m23| * |v2|
|u3| |m31 m32 m33| |v3|
the calculation is done as :
u1 := m11*v1 + m12*v2 + m13*v3
u2 := m21*v1 + m22*v2 + m23*v3
u3 := m31*v1 + m32*v2 + m33*v3
a short notation : ui := mij*vj = { sum(mij*vj) over j }
We'll have a closer inspection. Use the base vectors E1,E2,E3 as input and we see that the
columns in the matrix are the resulting vectors :
E1 -> (m11,m21,m31)
E2 -> (m12,m22,m32)
E3 -> (m13,m23,m33)
meaning : the columns show us how the base is transformed.
matrix multiplication
two matrices can be multiplied as:
H:=M*N
|h11 h12 h13| |m11 m12 m13| |n11 n12 n13|
|h21 h22 h23|:= |m21 m22 m23| * |n21 n22 n23|
|h31 h32 h33| |m31 m32 m33| |n31 n32 n33|
calculated as :
h11 := m11*n11 + m12*n21 + m13*n31
h12 := m11*n12 + m12*n22 + m13*n32
h13 := m11*n13 + m12*n23 + m13*n33
h21 := m21*n11 + m22*n21 + m23*n31
h22 := m21*n12 + m22*n22 + m23*n32
h23 := m21*n13 + m22*n23 + m23*n33
h31 := m31*n11 + m32*n21 + m33*n31
h32 := m31*n12 + m32*n22 + m33*n32
h33 := m31*n13 + m32*n23 + m33*n33
or
hij := mik * nkj = { sum( mik * nkj ) over k }
note :matrices do generally not commute : N*M != M*N
Rotations
rotational matrices belong to the few reversible transformations, their determinating
value is 1, also meaning the length of a vector is preserved.
There is one matrix for each rotation and each angle, only the anlge can be parametrized.
The rotation is always around the origin. Off center rotations require first shifting the
origin, then the object is rotated, then shifted back.
Rotation around X
let's build a rotation around the X axis (=E1). This means the x component of a vector
is left unchanged :
|1 0 0 |
Rx(phi)= |0 cos(phi) sin(phi)|
|0 -sin(phi) cos(phi)|
simple, isn't it.
Rotation around Y
A rotation around Y (=E2) leaves the y component of a vector unchanged :
|cos(phi) 0 sin(phi)|
Ry(phi)= |0 1 0 |
|-sin(phi) 0 cos(phi)|
Rotation around Z
A rotation around Z (=E3) leaves the z component of a vector unchanged :
|cos(phi) sin(phi) 0|
Rz(phi)= |-sin(phi) cos(phi) 0|
| 0 0 1|
Arbitrary rotations
Arbitrary rotations can be achieved by a sequence of the above rotations, while
due to the non-commutive nature, the correct sequence has to be followed.
A general rotation can be expressed as :
|r11 r12 r13|
Rarb := |r21 r22 r23|
|r31 r32 r33|
as mentioned above, the columns are the new base (E1',E2',E3'). Thus
|cos(E1,E1') cos(E2,E1') cos(E3,E1')|
Rarb := |cos(E1,E2') cos(E2,E2') cos(E3,E2')|
|cos(E1,E3') cos(E2,E3') cos(E3,E3')|
perhaps, the coefficients are to be swapped over the diagonal ..
There may be a simpler way, though. A few centuries ago, Euler, a swiss mathematician
discovered it. It is sufficient to use 3 angles to describe any rotation, these angles
are called 'Euler's angles'.
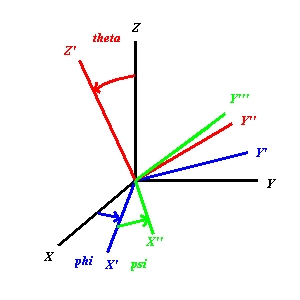
It is done as :
- rotate around Z by the angle phi(blue), this gives (X'(blue),Y'(blue),Z(black))
- rotate around X' by the angle theta(red), this gives (X'(blue),Y''(red),Z'(red))
- rotate around Z' by the angle psi(green), this gives (X''(green),Y'''(green),Z'(red))
The appropriate matrix is :
|cos(phi)cos(psi)-sin(phi)cos(theta)sin(psi) cos(phi)*sin(psi)+sin(phi)*cos(theta)*cos(psi) sin(phi)*sin(theta)|
Reuler(phi,theta,psi) := |-sin(phi)*cos(psi)-cos(phi)*cos(theta)*sin(psi) -sin(phi)*sin(psi)+cos(phi)*cos(theta)*cos(psi) cos(phi)*sin(theta)|
|sin(theta)*sin(psi) -sin(theta)*cos(psi) cos(theta) |
as can easily be verifyed by applying the appropriate rotations.
home
last updated: 6.nov.99
Copyright (99,2000) Ing.Büro R.Tschaggelar

