
linear feedback shift registers LFSR
LFSRs are commonly used to generate pseudo random bitstreams.
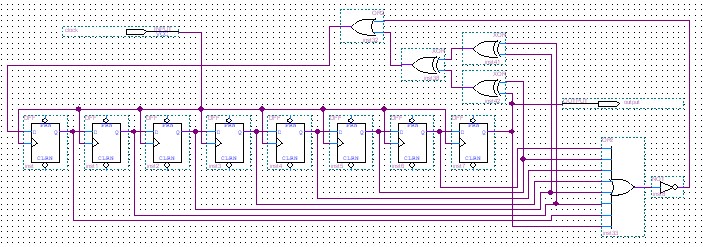
A LFSR is a shift register where arbitrary intermediate bits are fed back
by using an XOR with them and the shift register output.
Notice that the state where all Flipflops are zero is prohibited and
the NOR-ing of all intermediate bits enforces that.
properties
Noteworthy properties of the LFSR with the length N bits are
- the maximum non-repeating bitstream is 2^N -1 when the taps are well choosen.
- the maximum number of identical subsequent bits (0 or 1) is N
- the lowest contained frequeny is clock / N
- the highest contained frequency is the clock
The above properties are well understood and verified. When requiring
a parallel output eg for a DAC, no reference to properties was found.
for further information about practical implementations, have a look at
the Xilinx Application notes 210, 211, 217 & 220 ( XApp210.pdf, XApp211.pdf,
XApp217.pdf, XApp220.pdf ) to be found at Xilinx
simulating a parallel LFSR
Be the LFSR of n bits of which m are used as parallel output.
The questions asked for the simulation :
- the longest possible cycle
- the distribution of parallel values
- the minimum contained frequency
- the maximum contained frequency
Some observations :
for the output width being equal the shift register length :
- each value except zero is being read out, this means the value
distribution is flat
- Since each value is different, it can be assumed the highest
frequency is the clock
- Since the sequence repeats after at most 2^n, this is the lowest
freqency available
for the output width being shorter than the shift register length :
- As the output values are truncated they repeat twice for
each missing bit
- While in the n=m setup each value may appear just once per
maximum cycle, in the n>m setup each value may appear n/m times.
- the distribuution of values is still flat
for sequences shorter than the maximum length :
- the distribution is still flat, but some values are missing,
and they appear to form a pattern - to be examined
- the sequence repeats as often as the sequence is shorter
detailed research
general proofs may be made with induction.
I'll look into that when time permits.
simulations
home
last updated 26.june.03 or perhaps later
Copyright (99,2003) Ing.Büro R.Tschaggelar

